Сказка о стойкости
1982
Моя первая встреча с этими лабиринтами была около 1982 года, когда лабиринт Жан-Луи Буржуа показал мне игру в лабиринт. Он сказал мне, что эта игра широко распространена в народных культурах Азии; он очень стар, так как этот самый дизайн имеет место на критских монетах IV-V вв. до н.э., где он символизирует Лабиринт, в котором хранился Минотавр. (На самом деле, есть намного более ранние примеры). Согласно легенде, Тесей нашел выход из лабиринта, следуя нитью, которую он размотал из катушки, подаренной ему его возлюбленной Ариадней, и поэтому линия, нарисованная так, чтобы проследить путь через такой лабиринт часто называют «нитью Ариадны».
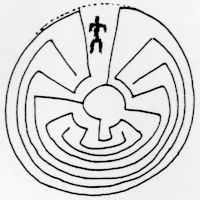
Спустя короткое время я посетил дом Дэвида Гей, математика в Университете Аризоны в Тусоне. На стене висела плоская корзина диаметром около 18 дюймов, сплетенная с дизайном, который оказался топологически идентичным критскому лабиринту. Дэвид сказал мне, что этот дизайн корзины является традиционным с индейцами To’ono-Otum (ранее «Papago»), племенем, живущим сейчас в северной Аризоне, и что повороты пути через лабиринт представляют собой события и испытания в жизни героя Иитоя, показанного у входа.
1983
Наконец, несколько месяцев спустя, посетив моих родителей во Флориде и перелистывая каталог Sotheby’s, меня поразила фотография страницы из средневековой рукописи Иврита (Sefer Haftorot), которая должна была быть продана 23 июня 1983 года. На фотографии была показана эта конструкция:

Семь концентрических стен символизируют семь стен Иерихона. Слова Псалма 104, ст. 1-18, 20, 21 ветер вдоль пути. В центре написано «Джерихо» и «Образ стены Иерихона». Читатель, как ходьба ». (Спасибо профессору Роберту Голдбергеру за перевод.) Фото предоставлено Sotheby’s Inc., Нью-Йорк.
Хотя этот лабиринт имеет поверхностное сходство с критским лабиринтом, близкое сравнение показывает, что они совершенно разные. Лабиринт Иерихона имеет 7 уровней, тогда как критский лабиринт имеет 8, и последовательность, в которой достигнуты уровни, сильно отличается от одного лабиринта к другому. В обоих лабиринтах путь идет прямо к уровню 3 (считая снаружи как 0), но в критском лабиринте он затем удваивается обратно через уровни 2 и 1, тогда как в лабиринте Иерихона он продолжается через уровни 4 и 5, прежде чем вернуться к 2 и 1. Полные последовательности уровней
Критский 0 3 2 1 4 7 6 5 8
Иерихон 0 3 4 5 2 1 6 7.
Их можно интерпретировать как музыкальные фразы, давая 0 = C, 1 = D и т. Д. Ухо сразу обнаруживает, что в критской мелодии исходная фраза повторяется с более высоким шагом; как я понял позже, этот лабиринт можно разложить на произведение или штабелирования две копии четырехуровневого лабиринта 03214.
Увидев два похожих, но разных примера, я начал задаваться вопросом, сколько еще может быть. Первым делом было понять, что у них общего. Оказывается, есть три характеристики, которыми они разделяют, и которые определяют класс лабиринтов, которые могут быть исследованы математически: это простые, чередующиеся транзитные лабиринты. Меня заинтересовала проблема определения M (n), числа различных s.a.t. лазурит с n уровнями.
1985-86
К тому времени я проводил отпуск в Италии, где Мишель Эммер, профессор Римского университета, делал одно из своих фильмов Math / Art, посвященное лабиринтам. Он пригласил меня появиться в фильме и поговорить о s.a.t. лазурит, поэтому я написал для себя сценарий, который является основой этого текста. В сценарии я объяснил, как вы узнаете, какие перестановки целых чисел могут быть уровнями последовательностей s.a.t. лабиринты. (Это ушло из фильма.)
1986
В декабре 1986 года я наткнулся на Пола Эрдеша на вечеринке и рассказал ему о моем интересе к этому комбинаторному феномену. Он спросил меня, увеличилось ли число M (n) экспоненциально или даже факториально с n. Этот короткий разговор заставил меня задуматься о поведении функции M (n). Через неделю я смог написать ему, что число I (n) интересных лабиринтов возрастает, по крайней мере, экспоненциально с n. Доказательство по построению показывает, что I (n + 4)> = 6I (n); 6 можно улучшить до 8 следующим образом: для каждого интересного лабиринта четной глубины n показаны восемь (n + 4) уровней лабиринтов
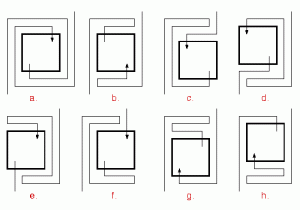
все это интересно, и эти новые лабиринты различны. На этом рисунке лабиринты представлены их лабиринтами в прямоугольной форме. Обратите внимание, что оригинальный лабиринт n-уровня происходит как с его входом справа, так и слева. Доказательство того, что эти лабиринты различны, требует гипотезы «интересной».
Затем я начал искать способ вычисления M (n). Метод, который я использовал, не был практичен при больших значениях n, поскольку он включал просмотр ряда пар перестановок, которые увеличивались, примерно, как ((n / 2)!) ^ 2. Например, для вычисления M (20) потребовалось бы изучение примерно 10 ^ (13) пар, что потребовало бы длительного времени даже на очень быстром компьютере. Помощь прибыла из неожиданного источника.
1987
В разделе «Наука Нью-Йорк Таймс» во вторник, 27 января 1987 года, была статья Джеймса Глейка о математике Нейле Дж. А. Слоане, который начался: «Не имея никакого значения, Нил Дж. А. Слоан стал мировым клиринговым центром для числовых последовательностей , Он отслеживает легкие, как 1, 2, 4, 8, 16, 32 …, полномочия двух. Он отслеживает жесткие, как 1, 1, 2, 5, 14, 38, 120, 353 …, количество различных способов складывания вечно более длинных полос почтовых марок. … ”
Это было первое, что я когда-либо слышал о проблеме сгибания штампа, но это явно связано с проблемой подсчета лабиринтов. Фактически каждый лабиринт глубины n дает способ складывания полосы из n + 1 штампов: поместите лабиринт в прямоугольную форму и проложите маркеры вдоль пути лабиринта, по одному на каждом уровне (включая 0 и n), игнорируя вертикальную сегменты. Но есть разница: первая и последняя марки сложенной полосы могут иметь свои свободные края, встроенные внутрь пакета, в то время как первый уровень (после 0) и последний уровень (до n) пути лабиринта должны имеют свои свободные концы снаружи. Поэтому, если F (n) – количество способов складывания полосы из n штампов, мы можем заключить только, что M (n) <F (n + 1).
Вычисление F (n) было сделано Джоном Э. Келером, SJ при n <= 16 в статье, опубликованной в 1968 году. Числа начинаются, как указано выше, и поднимаются до F (16) = 4215768. Но наиболее полезным было что Келер описал способ подсчета складков полосы из n штампов (n четный), посмотрев на пары «n-шаблонов», а число отдельных n-образных шаблонов было доступно в закрытой форме, для n четных: it (n / 2) -е каталонское число Cat (n / 2). Сидел. лабиринты с n уровнями допускают аналогичное перечисление; в этом случае два n-образных шаблона должны удовлетворять дополнительному условию, которое гарантирует, что один путь пронизывает весь лабиринт. Теперь каталанские числа, даже если они определены с факториалами, растут только экспоненциально; на самом деле
k -3/2 -1/2
Cat (k) ~ 4 k pi
для k больших, легкое следствие формулы Стирлинга. Из этого следует, что, поскольку каждый лабиринт n-уровня соответствует паре n-образных шаблонов, число M (n) лабиринтов n-уровня (n четное) составляет <= Cat (n / 2) ^ 2 и поэтому растет не более экспоненциально.
Более практично, существует гораздо меньше пар n-образных шаблонов, чем пар перестановок n / 2 элементов, и идентификация Келера позволила мне вычислить M (n) через n = 22 для n четных, проверив все пары n-шаблонов для однотактное свойство. Разумеется, время вычисления все равно экспоненциально возрастает с n. При n = 22 число пар n-образных шаблонов, подлежащих исследованию, было Cat (11) ^ 2 = 3455793796. Это заняло около 73 часов на компьютере Sun-3. Расчет n = 24 займет примерно 16 раз и т. Д.
Джим Ридс из Bell Labs нашел лучший метод и смог расширить вычисление до n = 28.
Одним из побочных продуктов моего изучения этих моделей лабиринта была осознание того, что лабиринты древних времен работали путем объединения ограниченного числа фундаментальных форм. Это позволило мне предположить, как следует восстановить частично разрушенные римские мозаичные лабиринты и обнаружить некоторые примеры ошибочной реставрации у тех, кто уже отремонтирован. См. Топология римских мозаичных лабиринтов.
Вернуться на главную страницу лабиринта
Вернуться на главную страницу Тони
Origional Source: http://www.math.stonybrook.edu/~tony/mazes/motivation.html
