Table of Contents
1. Introducción:
La creación de esta página fue provocada por las discusiones en el grupo de noticias rec.sport.rowing sobre por qué el remo río arriba o río abajo se siente diferente, y también la diferencia entre aguas profundas / poco profundas. Comenzaré diciendo que estoy asumiendo que remar corriente abajo se siente ‘más pesado’ que remar río arriba, lo cual es mi impresión personal, aunque algunos dirían que es al revés, lo cual no puedo explicar excepto como un efecto puramente psicológico. Además, estoy descartando el cambio en la resistencia del aire, es decir, cuando remas río abajo, siempre te mueves más rápido en relación con el aire que remar río arriba, por lo que relativamente, las piezas aguas abajo son más viento en contra que las aguas arriba. Esto es claramente correcto pero, creo, insignificante. De nuevo, personalmente, creo que puedo ver la diferencia entre una mayor resistencia al agua y una mayor resistencia del aire, y la diferencia aguas arriba / aguas abajo me parece una resistencia al agua.
2. Viscosidad:
Considere dos superficies separadas por fluido, una distancia H aparte, con la superficie superior moviéndose en V y la superficie inferior fija. El fluido adyacente a la superficie superior se arrastrará y también se moverá a la velocidad V mientras que el fluido adyacente a la superficie inferior estará estacionario, de modo que se establece un gradiente de velocidad constante V / H (también conocido como “cortante”) en el fluido
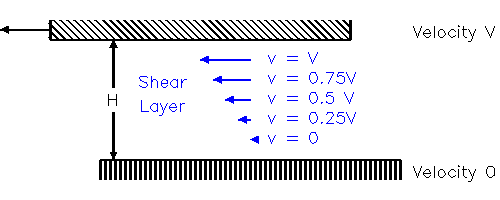
Como cualquier libro de texto de física le dirá, la Resistencia R (medida como fuerza por unidad de área) causada por la viscosidad viene dada por:
| (2.1) | R = e d v / d z |
donde e es el coeficiente de viscosidad (medido en kg / m / s, se supone constante), y el cortante dv / dz = V / H en este caso, por lo que
| (2.2) | R = eV / H |
Esto te dice que el arrastre viscoso (resistencia) en la superficie superior aumenta en proporción a la velocidad. Sin embargo, esto solo se aplica realmente a situaciones donde las longitudes horizontales son mucho mayores que la separación H, de modo que la capa de corte es constante a lo largo de toda la longitud. Esto solo es cierto para los barcos que reman sobre aguas muy poco profundas (pulgadas). Para la mayoría de los propósitos, se requiere un mejor modelo.
3. Resistencia del barco:
Cuando un bote se mueve a través de agua estacionaria, el agua en contacto con los arcos se acelera inmediatamente a la velocidad del bote V, pero la capa de cortante solo puede crecer hacia abajo a una velocidad fija W (establecida por el camino medio libre de moléculas). Por lo tanto, el límite inferior (estático) de la capa de corte se inclina hacia abajo desde los arcos:
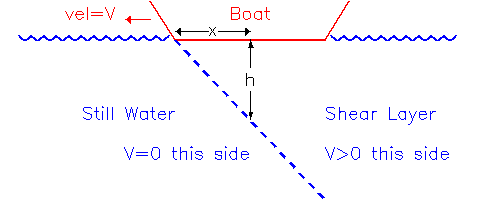
Debajo del punto x a lo largo del casco, la capa límite habrá crecido durante un tiempo t = x / V, por lo que habrá alcanzado una profundidad h = W.t = W.x / V. Entonces, usando la ecuación (2.1), la resistencia viscosa en el punto x viene dada por:
| (3.1) | R (x) = eV 2 / ( Wx ) |
Este es el origen de la ley V2 para la resistencia de la embarcación (véase la resistencia proporcional a V en la sección anterior) – ver la Sección 2 de Fundamentos
4. Corriente de río:
El flujo del río es impulsado por el gradiente de presión hidrostática, que es constante a través de toda la sección transversal del río. Si no fuera por los efectos de la viscosidad, esto significaría que la corriente fluye a una velocidad igual en todos los puntos dentro de la sección transversal, ya que cada punto se impulsa con la misma fuerza. Sin embargo, debido a la viscosidad, el flujo es más lento cerca del límite fijo (lecho y riberas) y más rápido cerca del límite libre (superficie, ya que el aire ofrece relativamente poca resistencia al flujo), y el flujo más rápido será el más alejado del fijo límite, que significa lejos de los lados y donde el río es más profundo.
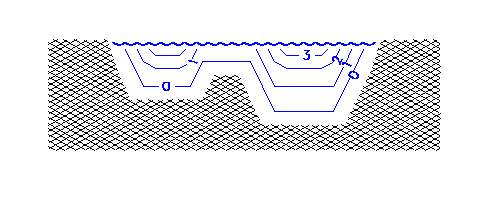
El diagrama muestra una sección transversal de flujo sobre un lecho de río desigual, los contornos representan la velocidad de flujo. El flujo es 0 al lado del límite fijo, 1 para 1 capa de distancia, y así sucesivamente. Como en la mayoría de los ríos, siendo más ancho que profundo, el caudal en la mayoría de los lugares está determinado por la profundidad más que por la distancia desde los lados. El flujo superficial es, por lo tanto, más rápido (3) sobre el canal derecho y más lento hacia los lados, o sobre el borde central.
5. Efecto del flujo del río en la resistencia:
Si hay algún flujo, la corriente tendrá su propia cizalladura vertical (diagrama de la izquierda en la Fig. 5.1). En la Sección 3, un barco que se mueve a través del agua quieta también establecerá su propia capa de corte en algún punto fijo debajo del casco (diagrama de la derecha).
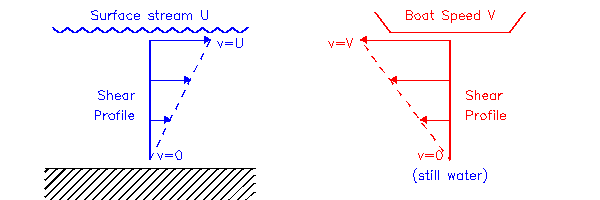
Cuando tenemos una embarcación moviéndose en una corriente, estas dos tijeras se sumarán como en la Fig. (5.2)
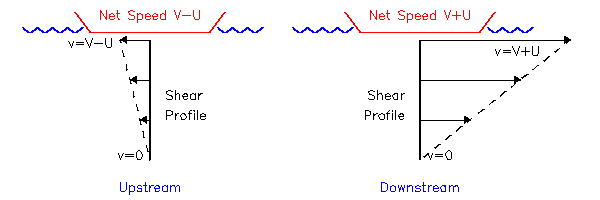
El diagrama de la izquierda muestra la cizalladura establecida por una embarcación que se mueve aguas arriba a la velocidad V en relación con el agua, que a su vez se mueve a la velocidad U con respecto al banco o al lecho del río. En este caso, hay alguna cancelación entre las dos capas de cizallamiento: la velocidad de cizalla debajo del barco se reduce por lo que hay menos arrastre aparente en comparación con la caja de agua sin gas. El diagrama de la derecha muestra la situación opuesta para un barco que se mueve río abajo. Aquí aumentan la cizalladura y la resistencia aparente.
En general, cuanto más rápido es el flujo, o cuanto menos profunda es la superficie del agua, mayor es la fuerza cortante, por lo que mayor es la diferencia de resistencia.
6. Resistencia al agua poco profunda:
La diferencia entre las secciones 2 y 3 fue que, en el primer caso, la capa de corte tenía una profundidad fija, mientras que en el último crecía continuamente a medida que el barco pasaba por encima.
En aguas poco profundas, la capa de cizallamiento puede tocar el fondo, en cuyo caso, obviamente, deja de crecer y se aplica la ecuación (2.2) en lugar de la ecuación (3.1). A primera vista, esto podría parecer algo bueno, ya que en la Ec. (2.2) el arrastre solo aumenta linealmente con la velocidad en lugar del cuadrado de la velocidad de la ecuación (3.1). Sin embargo, debe recordar que los efectos de fondo se sienten a bajas velocidades en lugar de altas (ya que la capa de corte tiene más tiempo para crecer hacia abajo a bajas velocidades) y el punto en el que las dos se igualan es donde la capa de corte se separa del fondo.
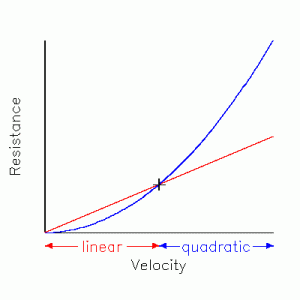
Entonces a bajas velocidades, la resistencia al agua superficial es lineal (mostrada por la línea roja en la figura 6.1) y mayor de lo que se esperaría del régimen cuadrático (mostrado por la línea azul) con una capa de cizalla sin límites. Cambiar la profundidad del agua tiene el efecto de reducir la pendiente del régimen lineal (diferenciando la ecuación (2.2)):
| (6.1) | d R / d V = e / H |
de modo que la transición (en el punto + en el diagrama) de lineal a cuadrática ocurre a velocidades más bajas.
Entonces, ¿qué tan superficial debe ser el agua antes de que notes el fondo? Puede hacerse una idea de la profundidad de la capa de cizalladura observando la extensión de la turbulencia lateral en la popa del barco (la capa de cizalladura probablemente crece hacia abajo a la misma velocidad que hacia afuera), es decir, alrededor de 1 metro. Más profundo y no deberías notar el fondo en absoluto. La profundidad mínima para los cursos de Regatta Olímpica es, creo, de 2 metros, solo para estar seguros.
Por supuesto, como la velocidad tiende a cero, la capa de cizallamiento se extenderá hasta el infinito, por lo que la profundidad real del agua siempre se ‘notará’ con el tiempo, pero generalmente a bajas resistencias que será imposible distinguir entre lineal y cuadrático regímenes.
Tenga en cuenta que el agua en movimiento también tendrá una cizalla inducida por flujo (sección 5), un efecto completamente separado. En ese caso (es decir, ríos), la profundidad total siempre será significativa.
7. Tiempos Río arriba/ Río abajo:
Es un concepto erróneo común que si rebasas, digamos, 2000 m corriente arriba y 2000 m corriente abajo, medido contra algunos puntos fijos en el banco, tu tiempo promedio es el mismo que si remaras 2000m en aguas tranquilas (estoy ignorando cualquier cambio en velocidad debido a la fatiga o los efectos discutidos en las secciones anteriores). Para velocidades de flujo bajas, es una aproximación razonable, pero el promedio en la corriente siempre será más lento que el tiempo de agua estancada. ¿Por qué? Porque…
Suponga que su velocidad intrínseca a través del agua es V, la velocidad de la corriente es U, y está remando una distancia L medida a lo largo del banco.
| (7.1) |
Tiempo de agua inmóvil, |
t S = L / V |
| (7.2) | Tiempo de subida, | t U = L / ( VU ) |
| (7.3) | Tiempo de bajada, | t D = L / ( V + U ) |
| (7.4) | Tiempo promedio, | t A = ½ ( t U + t D ) = LV / ( V 2 – U 2 ) |
Como era de esperar, como la velocidad de la corriente U tiende a cero, el promedio de tus tiempos (aguas arriba y aguas abajo) tiende hacia tu agua estancada, pero para cualquier corriente distinta de cero, tA es más larga que tS (porque V2-U2 siempre es menor que V2).
¿Qué diferente? Tome V = 5 m / s (correspondiente a tS = 6: 40 = 400 s, para 2000 m en agua inmóvil). Remando en un flujo (lento) de U = 10 cm / s, remaría 2000 m aguas arriba en tU = 408.2s, y río abajo en tD = 392.2s, dando un promedio de tA = 400.2s, es decir, solo 0.2s más lento, no importante. Pero en un flujo más rápido de U = 1 m / s, obtendrías tA = 416.7 s, es decir, 16.7 s, o pensarías que estás 5 longitudes más lento de lo que realmente eres. Tenga en cuenta que aunque la velocidad de la corriente aumentó en un factor de 10, el error aumentó en un factor de 100 (depende de U2).
Orignal source:
http://eodg.atm.ox.ac.uk/user/dudhia/rowing/physics/stream.html
